Es una sucesión infinita que empieza así:
1,1,2,3,5,8,13,21,34,55,89,144,233,377. . .
Una cosa bastante curiosa de ella es que los dos primeros números son el mismo (1 y 1). Más adelante os explicaré el porqué.
Se forma de la siguiente manera:
- Los dos primeros números son el 1
- Si sumas los dos 1 te da un 2
- Si sumas 1 + 2 te da el siguiente número: 3
- Si sumas 2+3 te da el 5
- Si sumas el 3+5 te da el 8
- . . .
Como veis la sucesión es infinita al estar formado cada elemento por la suma de los dos anteriores.
¿Quién la descubrió?
¿Fibonacci? Si y no. No es fácil decir quién la descubrió pero se sabe que quién la describió por primera vez en Europa fue Leonardo de Pisa o como también se llamaba, Fibonacci (este hombre fue un matemático italiano del siglo XIII).
¿Para qué se usa?
Si citamos textualmente a la Wikipedia:
"Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono."
Historia:
Antes de Fibonacci fue descubierta esta sucesión por matemáticos indios quienes habían descubierto que en los patrones rítmicos que se formaban en la formación de las sílabas o notas de uno o dos pulsos el número de tales ritmos era de ; por lo cuál se produce 0,1,1,2,3,5,8,etc
; por lo cuál se produce 0,1,1,2,3,5,8,etc
 ; por lo cuál se produce 0,1,1,2,3,5,8,etc
; por lo cuál se produce 0,1,1,2,3,5,8,etc
Un buen ejemplo que hicieron es el de la genealogía de unos conejos, que voy a poner aquí el ejemplo de la Wikipedia ya que es un buen ejemplo.
| Número de Mes | Explicación de la genealogía | Parejas de conejos totales |
|---|---|---|
| Fin del mes 0 | 0 conejos vivos. | 0 parejas en total. |
| Comienzo del mes 1 | Nace una pareja de conejos (pareja A). | 1 pareja en total. |
| Fin del mes 1 | La pareja A tiene un mes de edad. Se cruza la pareja A. | 1+0=1 pareja en total. |
| Fin del mes 2 | La pareja A da a luz a la pareja B. Se vuelve a cruzar la pareja A. | 1+1=2 parejas en total. |
| Fin del mes 3 | La pareja A da a luz a la pareja C. La pareja B cumple 1 mes. Se cruzan las parejas A y B. | 2+1=3 parejas en total. |
| Fin del mes 4 | Las parejas A y B dan a luz a D y E. La pareja C cumple 1 mes. Se cruzan las parejas A, B y C. | 3+2=5 parejas en total. |
| Fin del mes 5 | A, B y C dan a luz a F, G y H. D y E cumplen un mes. Se cruzan A, B, C, D y E. | 5+3=8 parejas en total. |
| Fin del mes 6 | A, B, C, D y E dan a luz a I, J, K, L y M. F, G y H cumplen un mes. Se cruzan A, B, C, D, E, F, G y H. | 8+5=13 parejas en total. |
| ... | ... | ... |
| Fin del mes 12 | ... | ... |
Nota: al contar la cantidad de letras distintas en cada mes, se puede saber la cantidad de parejas totales que hay hasta ese mes.
Más tarde otras personas investigaron en estos números, por ejemplo, el matemático escocés Robert Simson descubrió que la relación entre dos números sucesivos de Fibonacci era así:  y se acercaba mucho a la relación aúrea fi (
y se acercaba mucho a la relación aúrea fi ( ). Además cuanto más cercano a infinito fuera los dos números sucesivos de Fibonacci más exacta era la relación aúrea fi (por cierto,más adelante en otro post os explicare esta relación).
). Además cuanto más cercano a infinito fuera los dos números sucesivos de Fibonacci más exacta era la relación aúrea fi (por cierto,más adelante en otro post os explicare esta relación).
 y se acercaba mucho a la relación aúrea fi (
y se acercaba mucho a la relación aúrea fi ( ). Además cuanto más cercano a infinito fuera los dos números sucesivos de Fibonacci más exacta era la relación aúrea fi (por cierto,más adelante en otro post os explicare esta relación).
). Además cuanto más cercano a infinito fuera los dos números sucesivos de Fibonacci más exacta era la relación aúrea fi (por cierto,más adelante en otro post os explicare esta relación).
Usar la relación aúrea fi para hallar números de Fibonacci:
Sabiendo que la relación aúrea fi es de 1.618034... (aproximadamente) podemos calcular cualquier número de Fibonacci usando la razón de oro (la explicaré cuando explique el número fi):
Por ejemplo (ejemplo sacado de: http://www.disfrutalasmatematicas.com/numeros/fibonacci-sucesion.html):
Queriendo calcular el elemento número 6 de la sucesión (el 8) vemos que nos sale 8, en realidad sale 8.00000033 (pero es porque el fi es infinito por lo cual nunca nos saldrá exacto).
Bueno, en la próxima vez que os hable de este tema os hablaré sobre otras maneras de calcular los números de fibonacci, sus aplicaciones, el número fi y la razón de oro.
Hasta la próxima y si queréis saber más de esto d aquí: http://es.wikipedia.org/wiki/Sucesi%C3%B3n_de_Fibonacci
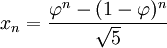







No hay comentarios:
Publicar un comentario